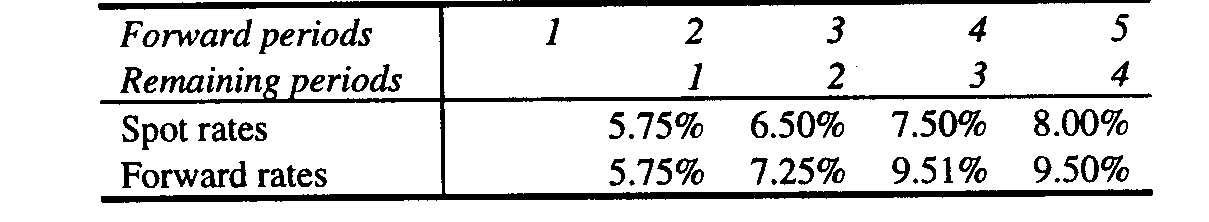Bob Jensen's Document on Interest Rate Swap Valuation, Forward Rate Derivation, and Yield Curves

In 2017 my Website was migrated to the clouds and reduced in size.
Hence some links below are broken.
Contact me at rjensen@trinity.edu if you really need to file that is missing.

Interest Rate Swap Valuation, Forward Rate Derivation, and Yield Curves
for FAS 133 and IAS 39 on Accounting for Derivative Financial Instruments

hardcover:
~~US$148 / £98 / S$196~~ US$111 / £73.50 / S$147
ebook:
~~US$111 / £74 / S$147~~ US$83.25 / £55.50 / S$110.25

From Wikipedia --- http://en.wikipedia.org/wiki/Yield_curve

In finance, the yield curve is the relation between the interest rate (or cost of borrowing) and the time to maturity of the debt for a given borrower in a given currency. For example, the current U.S. dollar interest rates paid on U.S. Treasury securities for various maturities are closely watched by many traders, and are commonly plotted on a graph such as the one on the right which is informally called "the yield curve." More formal mathematical descriptions of this relation are often called the term structure of interest rates.

The yield of a debt instrument is the annualized percentage increase in the value of the investment. For instance, a bank account that pays an interest rate of 4% per year has a 4% yield. In general the percentage per year that can be earned is dependent on the length of time that the money is invested. For example, a bank may offer a "savings rate" higher than the normal checking account rate if the customer is prepared to leave money untouched for five years. Investing for a period of time t gives a yield Y(t).

This function Y is called the yield curve, and it is often, but not always, an increasing function of t. Yield curves are used by fixed income analysts, who analyze bonds and related securities, to understand conditions in financial markets and to seek trading opportunities. Economists use the curves to understand economic conditions.

The yield curve function Y is actually only known with certainty for a few specific maturity dates, the other maturities are calculated by interpolation

In finance, the yield curve is the relation between the interest rate (or cost of borrowing) and the time to maturity of the debt for a given borrower in a given currency. For example, the current U.S. dollar interest rates paid on U.S. Treasury securities for various maturities are closely watched by many traders, and are commonly plotted on a graph such as the one on the right which is informally called "the yield curve." More formal mathematical descriptions of this relation are often called the term structure of interest rates.

The yield of a debt instrument is the annualized percentage increase in the value of the investment. For instance, a bank account that pays an interest rate of 4% per year has a 4% yield. In general the percentage per year that can be earned is dependent on the length of time that the money is invested. For example, a bank may offer a "savings rate" higher than the normal checking account rate if the customer is prepared to leave money untouched for five years. Investing for a period of time t gives a yield Y(t).

This function Y is called the yield curve, and it is often, but not always, an increasing function of t. Yield curves are used by fixed income analysts, who analyze bonds and related securities, to understand conditions in financial markets and to seek trading opportunities. Economists use the curves to understand economic conditions.

The yield curve function Y is actually only known with certainty for a few specific maturity dates, the other maturities are calculated by interpolation.

Continued in module

But the most important yield curve to derivatives salesmen is one you won't find in the financial pages --- the forward yield curve, or "forward curve." Actually, there are many forward curves, but all are based on the same idea. A forward curve is like a time machine: it tells you some point forward in time. Embedded in the current yield curve are forward curves of various forward times. For example, the "one-year forward curve" tells you what the current yield curve is predicting the same curve will look like in one year. The "two-year" forward curve tells you what the current yield curve is predicting the came cuve will look like in two years.
Frank Partnoy, Page 157 of Chapter 8 entitled "The Odd Couple"
F.I.A.S.C.O. : The Inside Story of a Wall Street Trader by Frank Partnoy
- 283 pages (February 1999) Penguin USA (Paper); ISBN: 0140278796
A longer passage from Chapter 8 appears at http://http://faculty.trinity.edu/rjensen/fraud.htm#DerivativesFraud

An interest rate swap is a transaction in which two parties exchange interest payment streams of differing character based on an underlying principal amount. As in all other swaps, the swap is a portfolio of forward contracts. Swaps are the most common form of hedging risk using financial instruments derivatives. Although forward contracting dates back prior to 200 B.C., interest rate swaps were invented in a swap deal put together by Salamon Brothers and Bankers Trust for IBM in 1984.

I suggest that readers commence with the fundamentals Basics are explained in the early part of "Summary of Derivative Types." This document also explains how to value certain types. It can be downloaded free from at http://www.rutgers.edu/Accounting/raw/fasb/derivsum.exe
Trinity students may find the file on the path J:\courses\acct5341\fasb\sfas133\derivsum22.doc

The most typical interest rate swaps entail swapping fixed rates for variable rates and vice versa. For instance, in FAS 133, Example 2 beginning in Paragraph 111 illustrates a fair value hedge and Example 5 beginning in Paragraph 131 illustrates a cash flow hedge. These are explained in greater detail in the following documents:

http://http://faculty.trinity.edu/rjensen/caseans/294wp.doc
The Excel workbook is at http://www.cs.trinity.edu/~rjensen/133ex02a.xls

http://http://faculty.trinity.edu/rjensen/caseans/133ex05.htm
The Excel workbook is at http://www.cs.trinity.edu/~rjensen/133ex05a.xls

A short tutorial on interest rate swaps is given at http://home.earthlink.net/~green/whatisan.htm. A good place to start in learning about how interest rate swaps work in practice is the CBOT tutorial at http://www.cbot.com/ourproducts/financial/agencystrat3rd.html. A very interesting (not free) swap calculator is given by TheBEAST.COM at http://www.thebeast.com/02_products/beast_help/ScreenSwapCalculator.htm
A tutorial can be found at http://www.thebeast.com/02_products/beastonline_gettingstarted.html

The two main types of interest rate swaps are coupon swap and basis swap. In a coupon swap or fixed-floating swap, one party pays a fixed rate calculated at the time of trade as a spread to a particular Treasury bond, and the other side pays a floating rate that resets periodically throughout the life of the deal against a designated index. In a basis swap or floating-to-floating swap is the swapping of one variable rate for another variable rate for purposes of changing the net interest rate or foreign currency risk. A basis swap (or yield curve swap) is an exchange of interest rates at two different points along the yield curve. This allows investors to bet on the slope of the yield curve. For example, an investor might arrange to borrow at six-month LIBOR but lend at the 10-year T-Bond rate, where interest rates are set twice each year. This swap is really two swaps combined: floating T-bill for floating T-bonds, plus a pure-vanilla swap between LIBOR and T-bills. Basis swaps are discussed in Paragraph 28d on Page 19, Paragraph 161 on Page 84, and Paragraphs 391-395 on Pages 178-179 of FAS 133.

The term "swap spread" applies to the credit component of interest rate risk. Assume a U.S. Treasury bill rate is a risk-free rate. You can read the following at http://www.cbot.com/ourproducts/financial/agencystrat3rd.html

The swap spread represents the credit risk in the swap relative to the corresponding risk-free Treasury yield. It is the price tag on the actuarial risk that one of the parties to the swap will fail to make a payment. The Treasury yield provides the foundation in computing this spread, because the U.S. Treasury is a risk-free borrower. It does not default on its interest payments.

Since the swap rate is the sum of the Treasury yield and the swap spread, a well-known statistical rule breaks its volatility into three components:

Swap Rate Variance = Treasury Yield Variance
+ Swap Spread Variance
+ 2 x Covariance of Treasury Yield and Swap Spread

Taken over long time spans (e.g., quarter-to-quarter or annual), changes in the 10-year swap spread exhibit a small but reliably positive covariance with changes in the 10-year Treasury yield. For practical purposes this means that as Treasury yield levels rise and fall over, say, the course of the business cycle, the credit risk in interest rate swaps tends to rise and fall with them.

However as Figure 1 illustrates, high-frequency (e.g., day-to-day or week-to-week) moves in swap spreads and Treasury yields tend to be uncorrelated. Their covariance is close to zero. Thus, for holding periods that cover very short time spans, this stylized fact allows simplification of the preceding formula into the following approximation:

This rule of thumb allows attribution of the variability in swap rates in ways that are useful for hedgers. For example, during the five years from 1993 through 1997, 99% of week-to-week variability in 10-year swap rates derived from variability in the 10-year Treasury yield. Variability in the 10-year swap spread accounted for just 1%.

The FAS 138 amendments to FAS 133 allow for benchmarking credit spreads. See Benchmark Interest Rate.

Basis risk arises when the hedging index differs from the index of the exposed risk. Examples might be the following: (1)The risk of loss from using a German mark position to offset Swiss franc exposure or using a shorter-termed derivative to hedge long-term interest rate exposures; (2) Exposure to loss from a maturity mismatch caused, for example, by a shift or change in the shape of the yield curve; (3) The variability of return stemming from possible changes in the price basis, or spread between two rates or indexes. This may also be called tracking error, correlation risk in some applications. The introduction of one European currency went a long way toward reducing basis risk in Europe.

A basis swap arises when one variable rate index (e.g., LIBOR ) is swapped for another index (e.g., a U.S Prime rate). Following the release of FAS 138, the FASB issued some examples. Note Example 1 in Section 2 of the FASB document entitled “Examples Illustrating Applications of FASB Statement No. 138” that can be downloaded from http://www.rutgers.edu/Accounting/raw/fasb/derivatives/examplespg.html. In Example 1 the basis swap entails a Euribor index basis swapped against US$ LIBOR. This illustrates the concept of a "basis swap spread" arising from swapping notionals in different currencies.

Interest rate swaps are illustrated in Example 2 paragraphs 111-120, Example 5 Paragraphs 131-139, Example 8 Paragraphs 153-161, and other examples in Paragraphs 178-186. See FAS 133 Paragraph 68 for the exact conditions that have to be met if an entity is to assume no ineffectiveness in a hedging relationship of interest rate risk involving an interest-bearing asset/liability and an interest rate swap. See yield curve, swaption, currency swap, notional, underlying, swap, legal settlement rate, and [Loan + Swap] rate. Also see basis adjustment and short-cut method for interest rate swaps.

One question that arises is whether a hedged item and its hedge may have different maturity dates. Paragraph 18 beginning on Page 9 of FAS 133 rules out hedges such as interest rate swaps from having a longer maturity than the hedged item such as a variable rate loan or receivable. On the other hand, having a shorter maturity is feasible according to KPMG's Example 13 beginning on Page 225 of the Derivatives and Hedging Handbook issued by KPMG Peat Marwick LLP in July 1998) states the following. A portion of that example reads as follows:

Although the criteria specified in paragraph 28(a) of the Standard do not address whether a portion of a single transaction may be identified as a hedged item, we believer that the proportion principles discussed in fair value hedging model also apply to forecasted transactions.

Interest Rate Swap Valuation since the Financial Crisis: Theory and Practice
SSRN, February 7, 2017
https://papers.ssrn.com/sol3/papers2.cfm?abstract_id=2912346

Authors

Ira G. Kawaller Kawaller & Company, LLC

Donald J. Smith Boston University - Department of Finance & Economics

Abstract

The financial crisis of 2007-09 revealed the importance of counterparty credit risk in the valuation of non-collateralized interest rate swaps. In theory, these valuations rest on assumed default probabilities and recovery rates. These assumptions, however, should be reflected in the risk-adjusted discount rates of the counterparties. Thus, in practice, swap valuations can be generated by discounting prospective swap settlements using risk-adjusted discount rates, cash flow by cash flow. This article demonstrates this method, discerning risk-adjusted discount rates from data that are readily available on the Bloomberg information system. Critically, if the inputs for the two methodologies are mutually consistent, theory and practice should yield identical valuations

"Larry Summers's Billion-Dollar Bad Bet at Harvard," by Matthew C. Klein, Bloomberg, July 18, 2013 ---
http://www.bloomberg.com/news/2013-07-18/larry-summers-s-billion-dollar-bad-bet-at-harvard.html

President Obama has only a few months to pick a candidate to replace Ben Bernanke as chairman of the Federal Reserve, and while the betting website Paddy Power has Fed Vice Chair Janet Yellen leading the pack at 1:4 odds, Larry Summers remains a strong contender at 11:2.

Despite an impressive resume that includes stints as Treasury Secretary and chief economist of the World Bank, there is a very good reason Summers shouldn't be in charge of monetary policy: He seems to have trouble with interest rates.

During the financial crisis, Harvard lost nearly $1 billion because of some unusual and ill-judged interest rate swaps that Summers implemented in the early 2000s during his troubled tenure as the university's president.

Interest rate swaps allow borrowers to lock in a fixed interest rate on floating-rate debt, which can be good to hedge against short-term uncertainty. The problem with Harvard was that Summers wanted to lock in interest rates for money that the university hadn't actually borrowed and wasn't planning on borrowing for a very long time.

There aren't a lot of ways to interpret this exotic instrument except as a bet that the future level of interest rates would be higher than the market pricing implied at the time. That bet was wrong, and Harvard lost a billion dollars. Anonymous finance blogger Epicurean Dealmaker puts it well:

"I have rarely encountered a corporate client who feels confident enough about both their absolute funding needs and current and impending market conditions to enter into a forward swap starting more than nine months into the future. Entering into a forward start swap for debt you do not intend to issue up to 20 years in the future sounds like either rank hubris or free money for Wall Street swap desks."

Why, back in 2004, did Summers feel so confident that interest rates were going to be much higher than they actually were? Reuters blogger Felix Salmon found one clue in a speech Summers gave in October of that year. Among other he things, Summers warned of the dangers created by the U.S. current account deficit and highlighted the seemingly absurd fact that short-term borrowing costs were lower than the rate of inflation. Perhaps Summers's experience with foreign-exchange crises in Asia and Latin America convinced him that something similar could happen in a country that borrowed in its own currency.

Not only was Summers wrong in 2004 about where interest rates would be -- he was willing to bet a lot of other people's money that he knew better than everyone else. The damage at Harvard was bad enough. Imagine what that sort of thing could do to the U.S. economy.

Working Paper 305

This paper was published in ”An Explanation of Example 5, Cash Flow Hedge of Variable-Rate Interest Bearing Asset in SFAS 133,” by Carl M. Hubbard and Robert E. Jensen, Derivatives Report, April 2000, pp. 8-13.
http://http://faculty.trinity.edu/rjensen/caseans/133ex05.htm
The Excel workbook is at http://www.cs.trinity.edu/~rjensen/133ex05a.xls

Some Corrections and Explanations of Example 5 in FAS 133

(March 10, 2000 Version)

Carl M. Hubbard and Robert E. Jensen

Trinity University

San Antonio, Texas

Introduction

Correcting the Errors and Explaining the Table

Discovering the Yield Curves

Summary, Conclusions, and Acknowledgements

Exhibits

In 1998, the Financial Accounting Standards Board (FASB) issued the derivatives and hedge accounting FAS 133 (or FAS 133) standard that will be one of the most costly and confusing of all FASB standards to implement.[i] This paper is the second of two papers that are intended to help readers cope with the two most difficult illustrations in FAS 133. The first paper on Example 2, which dealt with a fair value interest rate swap, was published in Derivatives Report, November 1999, pp. 6-11. With regard to Example 5 on pages 72 – 76 of FAS 133, which is supposed to demonstrate the mechanics of accounting for a cash flow interest rate swap, we contend that information necessary for understanding Example 5 was omitted and that the table on page 75 of FAS 133 contains a repeating error that that confounds attempts to understand the development of the example. In this paper we discuss and explain the table on page 75 of FAS 133 and correct the Interest accrued errors. We also supply yield curves that are consistent with swap values in the table on page 75 and demonstrate the calculation of expected swap cash flows from forward rates that are derived from the yield curves.

The data omitted from Example 5 are the yield curves that were used to calculate forward rates that in turn are used to calculate expected swap cash flows. The swap values at the reset dates in the table on page 75 are the present values of future expected swap cash flows that are discounted at rates in the unknown yield curves. This is unfortunate omission in FAS 133. The flat yield curve assumption for Example 2 allows readers to follow the example without information beyond that provided in our earlier paper, but the upward sloping yield curve assumption in Example 5 requires disclosure of the yield curve at each reset date in order to verify the swap values and understand the example. Our discussion of Example 5 begins with Paragraph 133 on page 73 of FAS 133. A companion paper will focus on Example 5 beginning in Paragraph 131.

Introduction to Example 5 in FAS 133

Example 5 focuses on an application of FAS 133 by XYZ Company that has entered into an effective, receive fixed/pay variable interest rate swap that extends over eight quarters. In the swap contract XYZ receives a fixed (6.65%) rate and pays a variable LIBOR rate on a notional principal amount of $10 million. This swap hedges the company’s expected cash flows from $10 million of notional principal that earns a floating annual rate of LIBOR + 2.25%. All payments and reset dates are quarterly beginning July 1, 20X1. Since XYX has entered into a receive fixed/pay variable swap, XYZ obviously is concerned that LIBOR rates would decline and thus reduce the income from the floating rate investment. Exhibit 1 below summarizes the facts assumed in the interest rate swap in Example 5.

Exhibit 1: Terms of the Interest Rate Swap and Corporate Bonds in Example 5

Interest Rate Swap Corporate Bonds

Trade date and borrowing date July 1, 20X1 July 1, 20X1

Termination date June 30, 20X3 June 30, 20X3

Notional amount $10,000,000 $10,000,000

Fixed interest rate 6.65% Not applicable

Variable interest rate 3-month US$ LIBOR 3-month US$ LIBOR

+ 2.25%

Settlement dates and interest End of each calendar End of each calendar

payment dates quarter quarter

Reset dates End of each calendar End of each calendar

quarter through quarter through

March 31, 20X3 March 31, 20X3

The above Example 5 has been modified somewhat by the March 3, 2000 FASB Exposure Draft No. 207-A containing several proposed amendments to FAS 133. However, the numerical outcomes and the Page 75 answers were not revised from the original Example 5 in FAS 133. We still see the need for proposing some corrections and explanations of the Page 75 results.

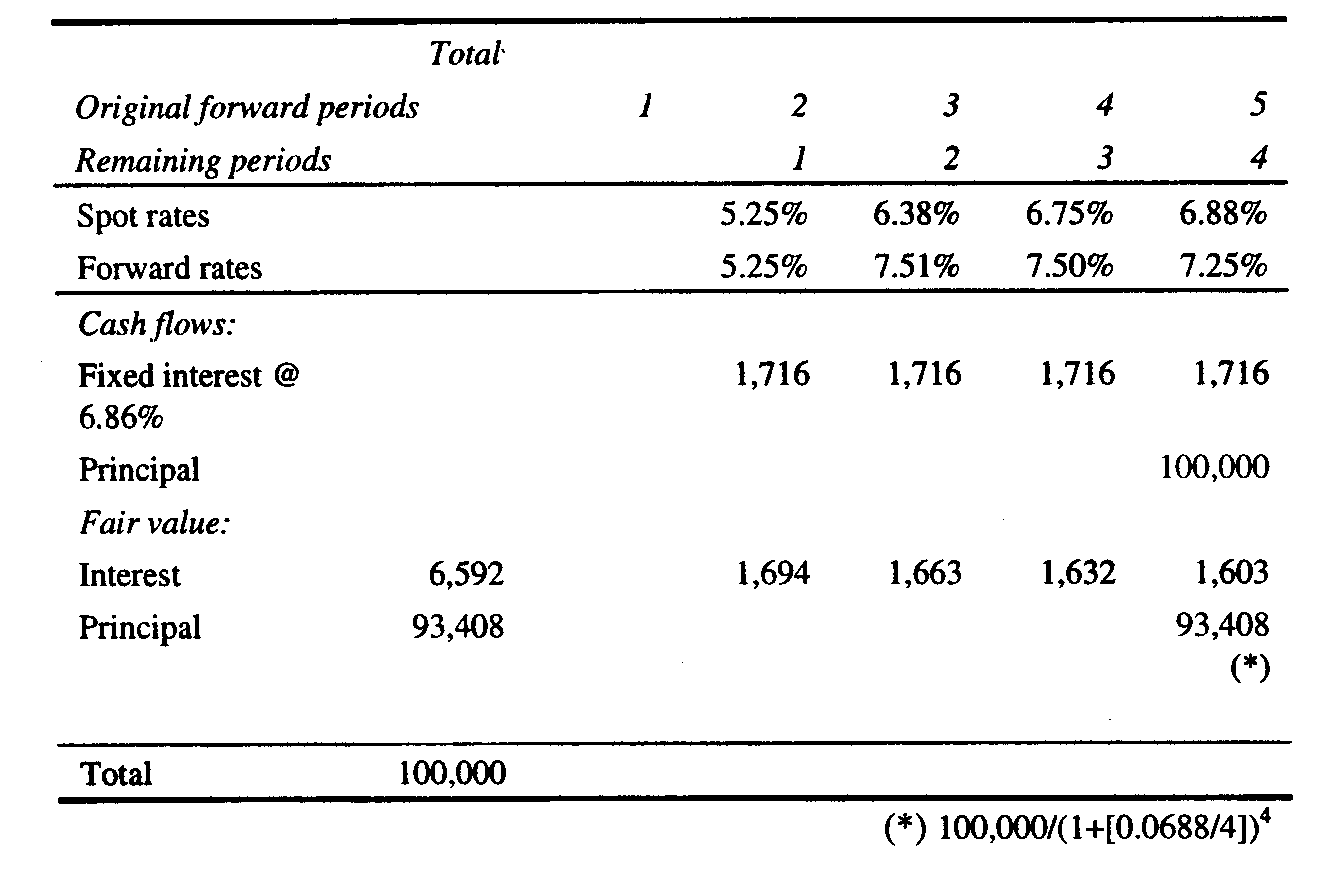
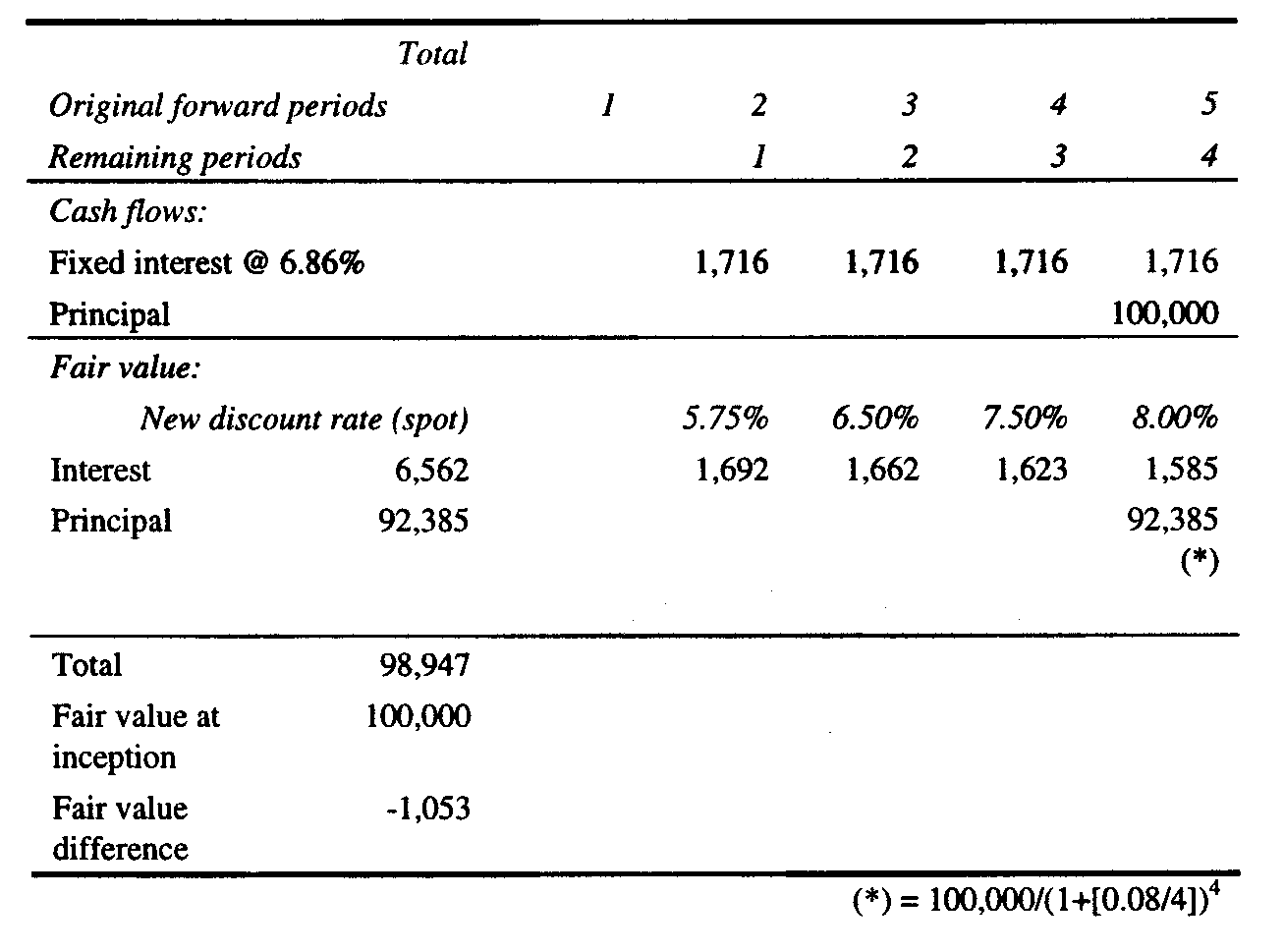
Correcting the Errors and Explaining the Table

The Interest Accrued amounts on Page 75 of FAS 133 are not compatible with the swap value and LIBOR rates at the reset dates. Either the Interest accrued amounts or the swap values are incorrect. For the reader’s convenience, the original table from page 75 of FAS 133 is reproduced in Exhibit 2 below. Our corrected version of the table is presented in Exhibit 3. Readers may download an Excel workbook, best read in Excel, with cell comments that compare the FASB's original Page 75 of FAS 133 with our corrected table from http://www.trinity/edu/rjensen/caseans/133ex05d.htm.

Insert Exhibits 2 and 3

Accepting the swap values as correct does less damage to the table, thus we assume the Interest accrued amounts must be corrected. Our Exhibit 3 reports the corrected Interest accrued amounts for each quarter using the LIBOR rates listed on page 74 of FAS 133. Since the initial present value of expected swap cash flows must be zero, the Interest accrued as of 9/30/X1 is correctly given as zero in the table on page 75 of FAS 133, in Exhibit 2, and Exhibit 3. By 9/30/X1 the LIBOR has changed, and the present value of expected swap cash flows beyond 9/30/X1 is revised to $24,850. The Interest accrued on $24,850 on 12/31/X1 is $350 or 0.0563/4 x $24,850. Thus in Exhibit 3 the Interest accrued amount for 12/31/X1 is corrected to show the $350 amount. Since the swap values are assumed to be correct in the original table, Effect of change in rates is adjusted also by the correction.

Again on 12/31/X1 the present value of expected swap cash flows is recalculated using an unspecified yield curve and is $73,800. The Interest accrued on $73,800 on 3/31/X2 is 0.0556/4 x $73,800 or $1,026, not $1,210 as presented in the original table. As before, the entry for Effect of change in rates is also adjusted. Because of changes in interest rates and because of the passage of time, the present values of expected swap cash flows change each quarter. Each quarter’s Interest accrued in Exhibit 3 is recalculated using the reset LIBOR at the beginning of the quarter, and as seen in Exhibit 3 each quarter’s entry for Effect of change in rates is also corrected.[ii]

The actual swap payments (receipts) as of the reset dates for the eight quarters are shown in Paragraph 138, page 76 of FAS 133. The payment (receipt) is equal to the variable LIBOR rate paid in the swap less the fixed rate received times the notional principle, or on 9/30/X1 (0.0556 – 0.0665)/4 x $10 million = ($27,250), a receipt. On 12/31/X1 the swap payment (receipt) is (0.0563 – 0.0665)/4 x $10 million = ($25,500). The swap cash flows are calculated in that same manner for each quarter throughout the life of the swap. Each quarter’s Effect of change in rates is equal to the current period’s recalculated value of the swap less the previous period’s swap value less the current period’s Interest accrued less the current period’s swap payment (receipt). In other words Effect of change in interest rates is the balancing item.

As shown in Exhibit 3, the effective swap terminates on 6/30/X3 with a zero value, and the 3/31/X3 present value of the one remaining swap cash flow is amortized by the swap payment (receipt) on 6/30/X3, the Interest accrued on the 3/31X3 value of the swap, and an accumulated rounding error, if any. We believer, therefore, that our Exhibit 3 is the correct presentation of entries related to Example 5.

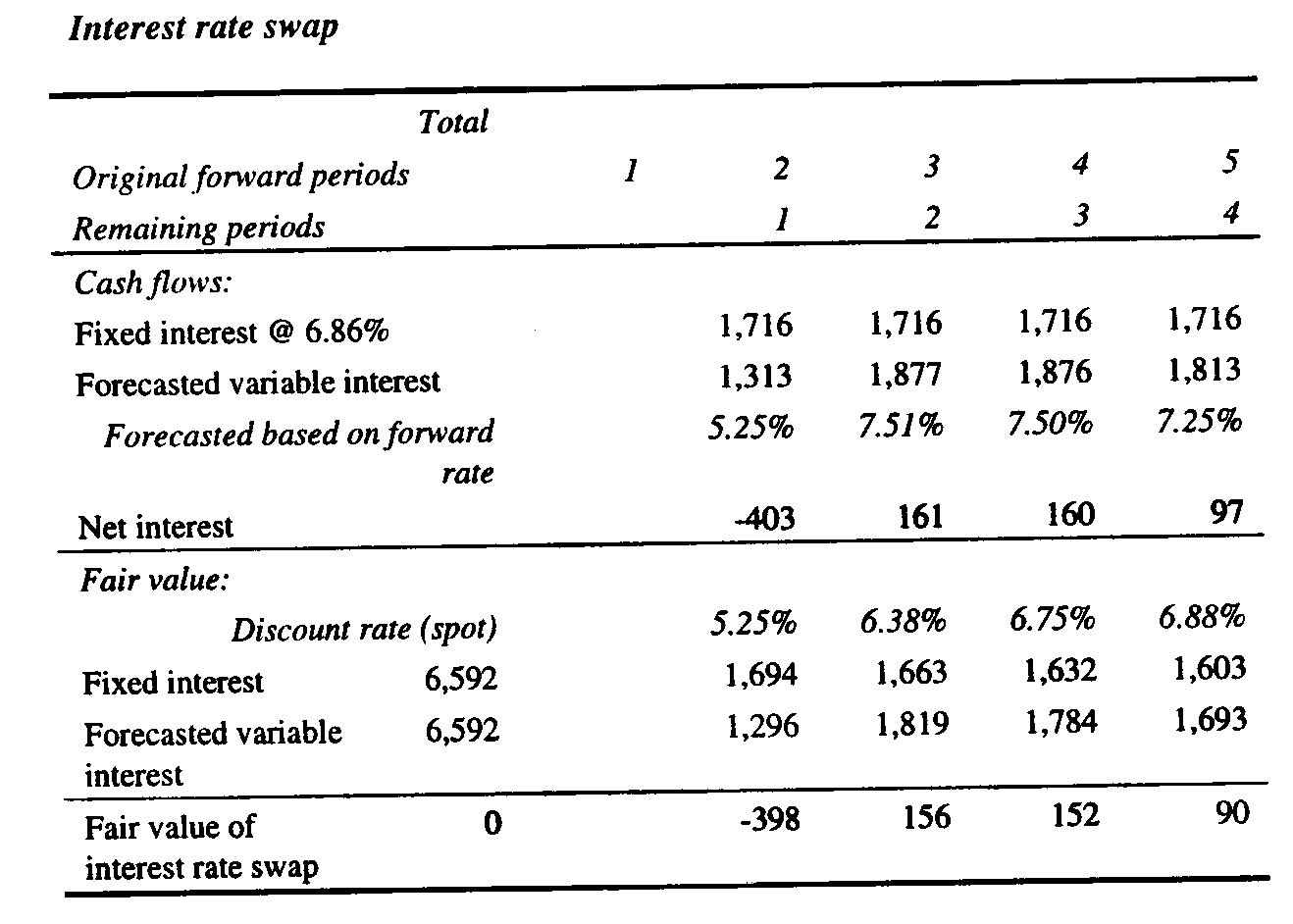
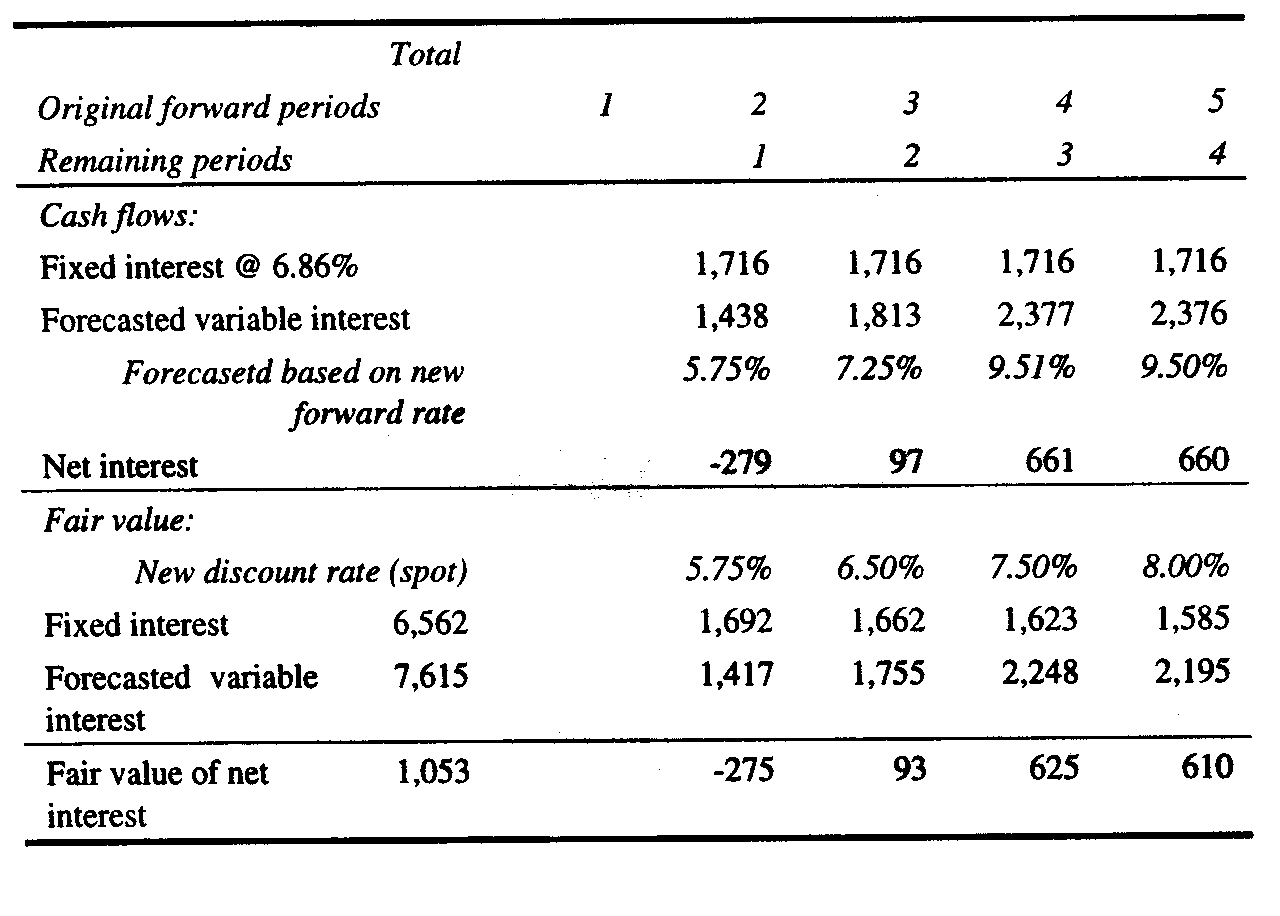
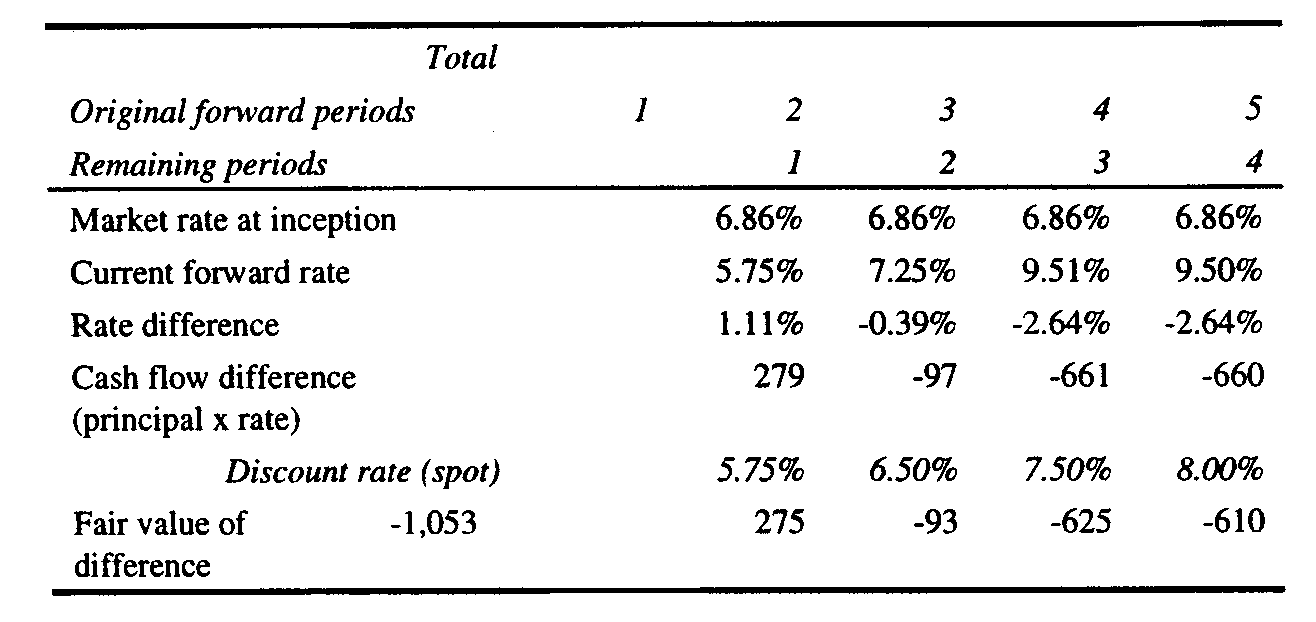
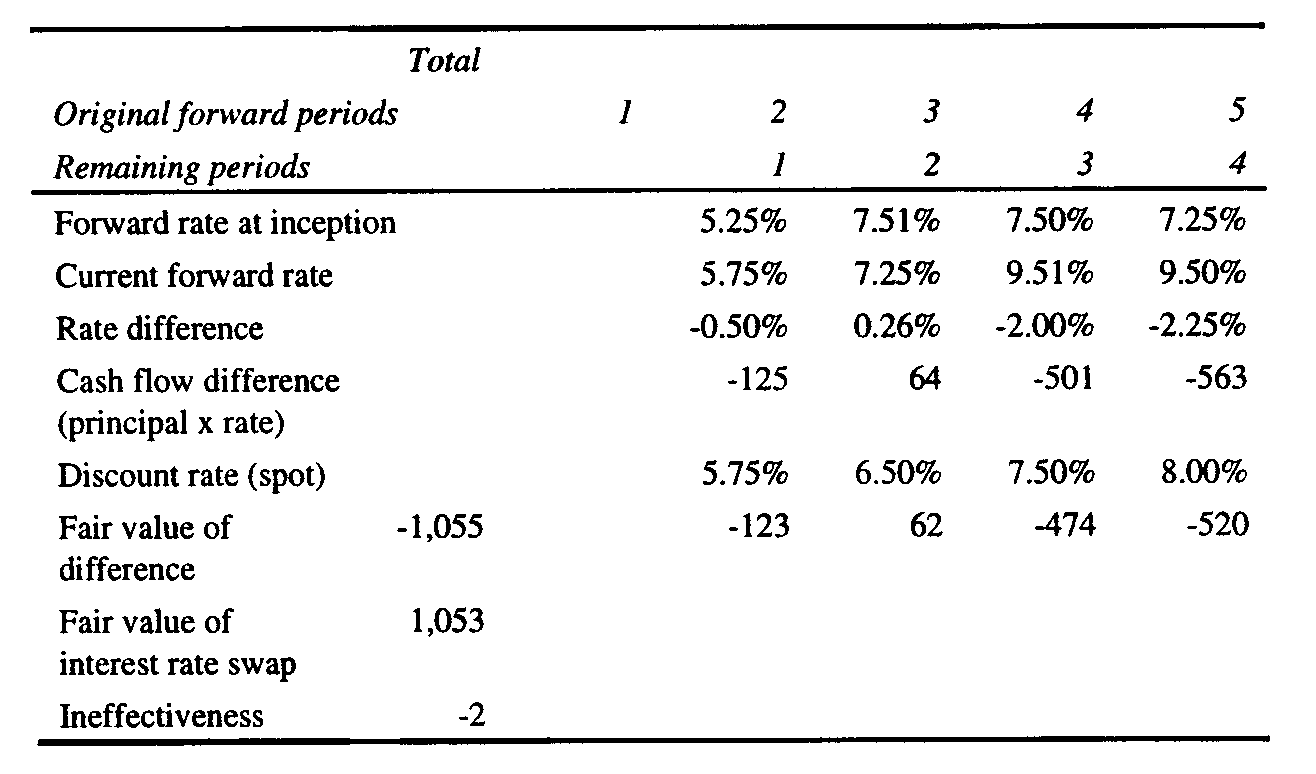
Discovering the Yield Curves

The underlying swap yield curves are unfortunately not disclosed by the FASB in Example 5. The swap values at the reset dates are the present values of the future expected swap cash flows. The cash flows that are discounted to the present value at each reset date cannot be known without the yield curves and the forward rates that are used to calculate the future quarterly expected cash flows. Furthermore, the discount rates that are used to calculate the values of the swap at the reset dates are the zero-coupon LIBOR’s that comprise the yield curves on the reset dates. Thus, in this example where an upward sloping yield curve is assumed, we must be given the yield curves at each reset date in order to replicate the calculations in the example. If we cannot easily replicate the example, it ceases to be an example in a pedagogical sense.

Nevertheless, we have discovered how the swap values on Page 75 of FAS 133 may have derived. In order to see how we derive yield curves that provide the same swap values given in the table on page 75 of FAS 133, the reader may wish to download the Excel workbook in Excel at http://http://faculty.trinity.edu/rjensen/caseans/133ex05a.xls and study the spreadsheet called "Effective." For this paper, we derived a yield curve at each reset date that provides the FASB’s swap values in the table on page 75 of FAS 133. We have some concerns as to whether the FASB’s swap values are theoretically sound, but that issue is reserved for another paper.

A yield curve is the graphic or numeric presentation of bond equivalent yields to maturity on debt that is identical in every aspect except time to maturity. In developing a yield curve, default risk and liquidity, for example, are the same for every security whose yield is included in the yield curve. Thus yields on U. S. Treasury issues are normally used to plot Treasury yield curves. The relationship between yields and time to maturity is often referred to as the term structure of interest rates. Similarly, an unknown set of estimated LIBOR yield curves underlie the FASB swap valuations calculated in Exhibit 3. Other than providing the assumption that the yields in the yield curves are zero-coupon rates, the FASB offers no information that would allow us to derive the yield curves or calculate the swap values in Example 5.

The typical yield curve gradually increases relative to years to maturity. That is, historically, short-term rates are somewhat lower than longer-term rates. In a recession with deflation or disinflation the entire yield curve shifts downward as interest rates generally fall and rotates counter-clockwise indicating that short-term rates have fallen to much lower levels than long-term rates. In rapid economic expansion accompanied by inflation, interest rates tend to rise and yield curves shift upward and rotate clockwise indicating that short-term rates have increased more than long-term rates. [iii]

The different shapes of the yield curve described above complicate the calculation of the present value of an interest rate swap and require the calculation and application of implied forward rates to calculate future expected swap cash flows. Fortunately Example 2 assumes that a flat yield curve prevails at all levels of interest rates. A flat yield curve means that as interest rates rise and fall, short-term and long-term rates move together in lock step, and future cash flows are all discounted at the same current discount rate. The cash flows and values in Example 5, however, are developed from the prevailing upward sloping yield curve at each reset date.

After reviewing the cases in Teets and Uhl, we used the tool Goal Seek in Excel to derive upward sloping yield curves and swap values at the reset dates that equal the FASB's values in the table on Page 75 of FAS 133.[iv] Exhibit 5 below shows the results of our calculations of the expected swap cash flows at each reset date and the value of the swap in Example 5 at each reset date. In order to see how we believe the swap values in the original table were derived for Example 5, the reader may wish to download the Excel workbook using Excel at http://http://faculty.trinity.edu/rjensen/caseans/133ex05a.xls and select “Effective.”

Insert Exhibit 4 here

In the development of Exhibit 4 we began with the derivation of a yield curve of LIBOR rates that provide a zero present value of future expected swap cash flows at the initiation of the swap. The only rate given in Example 5 for that first yield curve is 5.56% for the first quarter. Since the yield curve is upward sloping, we calculated a trial yield curve that begins at 5.56% and increases x% each quarter in the future. By supplying a value for x, we derived the trial yield curve and then calculated forward rates from that yield curve. The forward rates in this example are the future expected spot LIBOR rates that are implied by the zero-coupon rates in a yield curve. For example, assume that we have a two-year investment horizon and that the one-year LIBOR is 6.0% and the two-year LIBOR is 6.5%. If the LIBOR market is in equilibrium with respect to current rates and future expected rates, the 6.5% two-year rate must be the geometric mean of the one-year rate of 6.0% and the expected one-year rate beginning one year from now, which is 7.0%.

A forward rate is calculated in the following manner:

f(t) = [1 + r(t)]^t/[1 + r(t-1)]^t-1 – 1 (1)

in which f(t) is the forward rate for time period t, r(t) is the multi-period yield that spans t periods, and r(t-1) is the yield for an investment of t-1 periods. In the example above, 6.5% is r(t) and 6.0% is r(t-1). Thus, f(2), the forward LIBOR for year 2, is calculated as follows

f(2) = (1.065)²/1.06 – 1 = 0.07 or 7.0% (2)

Having calculated a forward rate for each quarter from the rates in the trial yield curve, we then asked Excel to give us the value of x, the slope of the upward sloping yield curve, that would provide a yield curve with forward rates that would calculate future expected swap cash flows whose present value is zero. The resulting yield curve, quarterly equivalent rates, forward rates, expected swap cash flows, and present values of cash flows as of 7/1/X1 are shown in the Panel 1 of Exhibit 4. A seen in Panel 1 of Exhibit 4, the first derived yield curve starts at 5.56% for the period ending 9/30/X1 and ends with a LIBOR of 6.68% for Eurodollar deposits maturing on 6/30/X3.

Future expected swap cash flows in Exhibit 4 are equal to the fixed rate received in the swap (0.0665/4) less the calculated forward rate times the notional principal. On 7/1/X1 in Example 5, the first quarter’s LIBOR of 5.56%/4 or 1.390% is also the first quarter’s forward rate, and the first period’s swap cash flow is (0.0665/4 - 0.0139) x $10 million = $27,250. The second quarterly forward rate is 1.470%, and the second quarter’s expected swap cash flow is (0.0665/4 - 0.0147) x $10 million = $19,265. The third quarterly forward rate is 1.550%, and so forth. When the thus calculated, the expected swap cash flows are discounted to the present value using the yields in the yield curve as discount rates. On 7/1/X1 the present value of the first swap cash flow of $27,250 is $27,250/1.0139 or $26,876. The present value of the second swap cash flow of $19,265 is $19,265/(1.0143²) or $18,725, and so forth through the remaining six quarters. As shown in Exhibit 4, the 7/1/X1 the initial sum of the present values of the eight expected swap cash flows is zero.

At the first reset date of 9/30/X1 in Example 5 the spot LIBOR increases to 5.63%. We derived the LIBOR yield curve for 9/30/X1 using Goal Seek in the same manner as described above. We asked Excel to calculate a value of x, the slope of the new yield curve beginning at 5.63%, that would give us a yield curve whose forward rates would provide swap cash flow calculations whose present value discounted at the yields in the yield curve equals $24,850. The results of those calculations are presented in the Panel 2 of Exhibit 4. We repeated that yield curve, forward rate, cash flow, and present value derivation process in Excel for each of the remaining reset dates in Example 5. The results of those derivations are given in Panels 3 through 8 of Exhibit 4. Since the interest rate swap is assumed to be effective, the concluding swap value on 6/30/X3 is zero.

Summary and Conclusions

Example 5 of FAS 133 is supposed to provide an example of accounting entries for a receive fixed/pay variable interest rate swap that that effectively hedges the variable interest income from an investment. However, the table on page 75 of FAS 133 is incorrect, and the information provided in Example 5 on the derivation of swap values is incomplete. The page 75 table reports Interest accrued amounts that are inconsistent with the given LIBOR rates and swap values. The LIBOR rates in the upward sloping yield curves that were used to derive forward rates, future expected swap cash flows, and swap values at the reset dates are not given in the example. Our objective in this paper was to correct the errors in the page 75 table, explain the entries in the corrected table, and then provide yield curves that are consistent with the swap values given in Example 5. We explain the derivation of trial yield curves, forward rates, swap cash flows, and swap values in Example 5. The corrected table in Exhibit 3 combined with the yield curve data and forward rates in Exhibit 4 enable a reader to understand the derivation of the cash flows, swap values, and other accounting entries that are the subjects of Example 5.

Readers may download an Excel workbook demonstrating our calculations from http://http://faculty.trinity.edu/rjensen/caseans/133ex05a.xls

Acknowledgments

We want to acknowledge the help from two individuals who independently found a calculation error in our first round of calculations. Thanks go to Peter van Amson from BankWare Inc and Dr. Walter R. Teets from Gonzaga University. Dr. Teets and his co-author, Robert Uhl, provide a free book online at at http://www.gonzaga.edu/faculty/teets/index0.html.

Peter van Amson sent us a corrected version of our own spreadsheet. He also recommended the following references:

For W.R.T. swaps the standard text used in practice is the Hull Book. Options, Futures and Other Derivatives, John C. Hull it has a fairly straight forward valuation of swaps. For an "advanced" actually just more mathematical treatment of the problem I recommend Interest Rate Option Models, Ricardo Rebonato.

The Hull reference is as follows: John C. Hull, Options, Futures, and Other Derivatives (Prentice-Hall, 1999, ISBN: 0130224448)

The Rebonato referernce is as follows: Ricardo Rebonato, Interest Rate Option Models (John Wiley & Sons, Wiley Finance, 1998, ISBN 0-471-96569-3)

Exhibit 2: Original Table in Example 5, FAS 133, Page 75

		Swap	OCI	Earnings	Cash
		Debit (Credit)	Debit (Credit)	Debit (Credit)	Debit (Credit)
July 1, 20X1		$ -

	Interest accrued	$ -
	Payment (Receipt)	(27,250)			27,250
	Effect of change in rates	52,100	(52,100)
	Reclassification to earnings	-	27,250	(27,250)	-
September 30, 20X1		24,850	(24,850)	(27,250)	27,250

	Interest accrued	$ 330	(330)
	Payment (Receipt)	(25,500)			25,500
	Effect of change in rates	74,120	(74,120)
	Reclassification to earnings	-	25,500	(25,500)	-
December 31, 20X1		73,800	(73,800)	(25,500)	25,500

	Interest accrued	$ 1,210	(1,210)
	Payment (Receipt)	(27,250)			27,250
	Effect of change in rates	38,150	(38,150)
	Reclassification to earnings	-	27,250	(27,250)	-
March 31, 20X2		85,910	(85,910)	(27,250)	27,250

	Interest accrued	$ 1,380	(1,380)
	Payment (Receipt)	(29,500)			29,500
	Effect of change in rates	(100,610)	100,610
	Reclassification to earnings	-	29,500	(29,500)	-
June 30, 20X2		(42,820)	42,820	(29,500)	29,500

	Interest accrued	$ (870)	870
	Payment (Receipt)	2,500			(2,500)
	Effect of change in rates	8,030	(8,030)
	Reclassification to earnings	-	(2,500)	2,500	-
September 30, 20X2		(33,160)	33,160	2,500	(2,500)

	Interest accrued	$ (670)	670
	Payment (Receipt)	5,250			(5,250)
	Effect of change in rates	6,730	(6,730)
	Reclassification to earnings	-	(5,250)	5,250	-
December 31, 20X2		(21,850)	21,850	5,250	(5,250)

	Interest accrued	$ (440)	440
	Payment (Receipt)	8,000			(8,000)
	Effect of change in rates	16,250	(16,250)
	Reclassification to earnings	-	(8,000)	8,000	-
March 31, 20X3		1,960	(1,960)	8,000	(8,000)

	Interest accrued	$ 40	(40)
	Payment (Receipt)	(2,000)			2,000
	Rounding error	-	-
	Reclassification to earnings	-	2,000	(2,000)	-
June 30, 20X3		$ -	$ -	$ (2,000)	$ 2,000

Exhibit 3: A Recalculation and Correction of the Interest Rate Swap in Example 5

			Swap	OCI	Earnings	Cash
LIBOR			Debit (Credit)	Debit (Credit)	Debit (Credit)	Debit (Credit)
5.56%	July 1, 20X1		$ -

		Interest accrued	$ -
		Payment (Receipt)	(27,250)			27,250
		Effect of change in rates	52,100	(52,100)
		Reclassification to earnings	-	27,250	(27,250)	-
5.63%	September 30, 20X1		24,850	(24,850)	(27,250)	27,250

		Interest accrued	$ 350	(350)
		Payment (Receipt)	(25,500)			25,500
		Effect of change in rates	74,100	(74,100)
		Reclassification to earnings	-	25,500	(25,500)	-
5.56%	December 31, 20X1		73,800	(73,800)	(25,500)	25,500

		Interest accrued	$ 1,026	(1,026)
		Payment (Receipt)	(27,250)			27,250
		Effect of change in rates	38,334	(38,334)
		Reclassification to earnings	-	27,250	(27,250)	-
5.47%	March 31, 20X2		85,910	(85,910)	(27,250)	27,250

		Interest accrued	$ 1,175	(1,175)
		Payment (Receipt)	(29,500)			29,500
		Effect of change in rates	(100,405)	100,405
		Reclassification to earnings	-	29,500	(29,500)	-
6.75%	June 30, 20X2		(42,820)	42,820	(29,500)	29,500

		Interest accrued	$ (723)	723
		Payment (Receipt)	2,500			(2,500)
		Effect of change in rates	7,883	(7,883)
		Reclassification to earnings	-	(2,500)	2,500	-
6.86%	September 30, 20X2		(33,160)	33,160	2,500	(2,500)

		Interest accrued	$ (569)	569
		Payment (Receipt)	5,250			(5,250)
		Effect of change in rates	6,629	(6,629)
		Reclassification to earnings	-	(5,250)	5,250	-
6.97%	December 31, 20X2		(21,850)	21,850	5,250	(5,250)

		Interest accrued	$ (381)	381
		Payment (Receipt)	8,000			(8,000)
		Effect of change in rates	16,191	(16,191)
		Reclassification to earnings	-	(8,000)	8,000	-
6.57%	March 31, 20X3		1,960	(1,960)	8,000	(8,000)

		Interest accrued	$ 32	(32)
		Payment (Receipt)	(2,000)			2,000
		Rounding error	8	(8)
		Reclassification to earnings	-	2,000	(2,000)	-
	June 30, 20X3		-	0	(2,000)	2,000

Exhibit 4: Calculation of Quarterly Values of the Interest Rate Swap in SFAS 133, Example 5

	LIBOR	Quarterly	Quarterly	Interest Rate Swap			Swap
Quarter	yield	LIBOR	forward	Receive	Pay	Swap	present
beginning	curve	rates	rates	6.65% fixed	LIBOR	cash flow	value
Panel 1:
07/01/01	5.56%	1.390%	1.390%	$ 166,250	$ 139,000	$ 27,250	$ 26,876
09/30/01	5.72%	1.430%	1.470%	166,250	146,985	19,265	18,725
12/31/01	5.88%	1.470%	1.550%	166,250	154,972	11,278	10,795
03/31/02	6.04%	1.510%	1.630%	166,250	162,961	3,289	3,098
06/30/02	6.20%	1.550%	1.710%	166,250	170,951	(4,701)	(4,353)
09/30/02	6.36%	1.590%	1.789%	166,250	178,942	(12,692)	(11,546)
12/31/02	6.52%	1.630%	1.869%	166,250	186,936	(20,686)	(18,473)
03/31/03	6.68%	1.669%	1.949%	166,250	194,930	(28,680)	(25,122)
Totals						$ (5,677)	$ 0
Panel 2:
09/30/01	5.63%	1.408%	1.408%	166,250	140,750	25,500	25,146
12/31/01	5.78%	1.445%	1.482%	166,250	148,153	18,097	17,586
03/31/02	5.93%	1.482%	1.556%	166,250	155,557	10,693	10,232
06/30/02	6.07%	1.519%	1.630%	166,250	162,962	3,288	3,095
09/30/02	6.22%	1.556%	1.704%	166,250	170,369	(4,119)	(3,813)
12/31/02	6.37%	1.593%	1.778%	166,250	177,777	(11,527)	(10,485)
03/31/03	6.52%	1.630%	1.852%	166,250	185,187	(18,937)	(16,911)
Totals						$ 22,995	$ 24,850
Panel 3:
12/31/01	5.56%	1.390%	1.390%	166,250	139,000	27,250	26,876
03/31/02	5.68%	1.419%	1.448%	166,250	144,825	21,425	20,829
06/30/02	5.79%	1.448%	1.507%	166,250	150,651	15,599	14,940
09/30/02	5.91%	1.477%	1.565%	166,250	156,478	9,772	9,215
12/31/02	6.03%	1.506%	1.623%	166,250	162,306	3,944	3,660
03/31/03	6.14%	1.536%	1.681%	166,250	168,135	(1,885)	(1,720)
Totals						$ 76,104	$ 73,800
Panel 4:
03/31/02	5.47%	1.368%	1.368%	166,250	136,750	29,500	29,102
06/30/02	5.59%	1.397%	1.426%	166,250	142,620	23,630	22,983
09/30/02	5.70%	1.426%	1.485%	166,250	148,492	17,758	17,020
12/31/02	5.82%	1.456%	1.544%	166,250	154,364	11,886	11,219
03/31/03	5.94%	1.485%	1.602%	166,250	160,236	6,014	5,586
Totals						$ 88,788	$ 85,910
Panel 5:
06/30/02	6.75%	1.688%	1.688%	166,250	168,750	(2,500)	(2,459)
09/30/02	6.87%	1.717%	1.746%	166,250	174,621	(8,371)	(8,091)
12/31/02	6.98%	1.746%	1.805%	166,250	180,493	(14,243)	(13,522)
03/31/03	7.10%	1.776%	1.864%	166,250	186,366	(20,116)	(18,748)
Totals						$ (45,230)	$ (42,820)
Panel 6:
09/30/02	6.86%	1.715%	1.715%	166,250	171,500	(5,250)	(5,161)
12/31/02	6.99%	1.746%	1.778%	166,250	177,768	(11,518)	(11,126)
03/31/03	7.11%	1.778%	1.840%	166,250	184,038	(17,788)	(16,872)
Totals						$ (34,556)	$ (33,160)
Panel 7:
12/31/02	6.97%	1.743%	1.743%	166,250	174,250	(8,000)	(7,863)
03/31/03	7.10%	1.775%	1.807%	166,250	180,738	(14,488)	(13,987)
Totals						$ (22,488)	$ (21,850)
Panel 8:
03/31/03	6.57%	1.643%	1.643%	166,250	164,258	1,992	1,960
Totals						$ 1,992	$ 1,960

Footnotes

[i] The reader may learn more about FAS 133 and other FASB standards at http://www.rutgers.edu/Accounting/raw/fasb/st/stpg.html. Also note the March 3, 2000 FASB Exposure Draft No. 207-A containing several proposed amendments to FAS 133 at http://www.rutgers.edu/Accounting/raw/fasb/draft/amend133_ED.pdf.

[ii] Accrued interest on the present value of future expected cash flow from the swap as of the end of the previous period for the eight quarters is calculated as follows:

9/30/X1: ($Swap value)(LIBOR/4) = ($0)(0.0556/4) = $0

12/31/X1: ($24,850)(0.0563/4) = $350

3/31/X2: ($73,800)(0.0556/4) = $1,026

6/30/X2: ($85,910)(0.0547/4) = $1,175

9/30/X2: (-$42,820)(0.0675/4) = ($723)

12/31/X2: (-$33,160)(0.0686/4) = ($569)

3/31/X3: (-$21,850)(0.0697/4) = ($381)

6/30/X3: ($1,960)(0.0657/4) = $32

[iii] See Chapter 6 “The Term Structure of Interest Rates” in James C. Van Horne Financial Market Rates and Flows, 5^th Edition. Upper Saddle River, NJ: 1998 for an excellent discussion of yield curves.

[iv] See “J. Adams and Company: Accounting for Interest Rate Swaps in an Upward Sloping Yield Curve Environment” in Introductory Cases on Accounting for Derivative Instruments and Hedging Activities, 1998, by Walter R. Teets and Robert Uhl. This case and other cases are available free online at http://www.gonzaga.edu/faculty/teets/index0.html.

In July 2001, IASB issued a consolidated document that includes all questions and answers approved in final form by the IAS 39 Implementation Guidance Committee as of 1 July 2001, including the fifth batch of proposed guidance (issued for comment in December 2000). The Q&A respond to questions submitted by financial statement preparers, auditors, regulators, and others and have been issued to help them and others better understand IAS 39 and help ensure consistent application of the Standard.

In November 2001, the IGC issued a document with the final versions of 17 Q&A and two illustrative examples that were issued in draft form for public comment in June 2001. That document replaces pages 477-541 in the publication Accounting for Financial Instruments - Standards, Interpretations, and Implementation Guidance, which was published in July 2001. Draft Questions 10-22, 18-3, 38-6, 52-1, and 112-3 were eliminated in the final document, primarily because the issues involved are being addressed in the Board’s current project to amend IAS 39. In November 2001, the IASB issued the following free document: