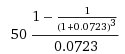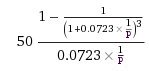http

In 2017 my Website was migrated to the clouds and reduced in size.
Hence some links below are broken.
One thing to try if a “www” link is broken is to substitute “faculty” for “www”
For example a broken link http://faculty.trinity.edu/rjensen/Pictures.htm
can be changed to corrected link http://faculty.trinity.edu/rjensen/Pictures.htm
However in some cases files had to be removed to reduce the size of my Website
Contact me at rjensen@trinity.edu if you really need to file that is missing

Working Paper 440
Annuities With Unequal Compounding and Payment Periods: The CFA Deconstruction Analysis
Bob Jensen at Trinity University

Before reading this you may want to peruse my document on the Wolfram Alpha Computational and Word Search Engine ---
Some Things You Might Want to Know About the Wolfram Alpha (WA) Search Engine: The Good and The Evil
as Applied to Learning Curves (Cumulative Average vs. Incremental Unit)
http://faculty.trinity.edu/rjensen/theorylearningcurves.htm

The discussion below is not about learning curves, but I will use the WA search engine.

Financial calculators and Excel financial formulas for computing present value, interim payments, and rates of return assume that p=m where p is the number of equally-spaced payments per year and m is the number equally-spaced interest compoundings per year. Complications introduced by p not being equal to m are not trivial problems. These complications are overlooked in many (probably almost all) mathematics of finance modules in both high school and college courses.

This note will demonstrate how to deal with complications when the number of payments per year is unequal to the number in times interest is compounded per year. This is not a purely academic problem. Companies buying and selling annuities often do not want to change the number of times interest is compounded every time they change the number of payments per year in a contract such as semi-annual payments versus quarterly payments versus monthly payments.

The paper was inspired by the following working paper sent to me by an Australian professor named Chris Deeley. Chris subsequently allowed me to put his paper on one of my Web servers:

"IDENTIFICATION AND CORRECTION OF A COMMON ERROR IN GENERAL ANNUITY CALCULATIONS"
by Chris Deeley,
Working Paper, Charles Sturt University, Australia, September 22, 2010
http://www.cs.trinity.edu/~rjensen/temp/DeeleyAnnuityCorrections.pdf
cdeeley@csu.edu.au

For illustrative purposes I will focus on the following example on Page 11 of Professor Deeley's working paper:

Example 2
A loan of $1million is to be repaid in equal monthly installments over four years. If the annual interest rate is 10% compounded semi-annually, how much is the monthly repayment?

The two solutions given by Professor Deeley for p=12 payments per year and m=2 interest compoundings per year are as follows:

Deeley Solution 1 PMT = $25,265.60 per month which Professor Deeley claims the "conventional solution"

Deeley Solution 2 PMT = $25,260.70 per month which Professor Deeley claims is his "proposed better solution"

I contend that there is a CFA Deconstruction and Rate Equivalence solution that I offer as an "alternate conventional solution" that is used of Certified Financial Analyst (CFA) examinations.

CFA Deconstruction PMT = $25,483 per month which conforms to David Frick's solution tutorial

David R. Frick Tutorials provides some outstanding mathematics of finance tutorials (free) --- http://www.frickcpa.com/

Time Value of Money Tutorials --- http://www.frickcpa.com/tvom/TVOM_Compound.asp

In particular I will focus on the following David Frick tutorial
Present Value of an Annuity Tutorial --- http://www.frickcpa.com/tvom/TVOM_PV_Annuity.asp#period

Before beginning my analysis below, I might point out that in his own illustration, David Frick has a somewhat misleading formula. The formula in his illustration reads as follows:

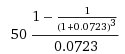
The formula of his illustration should read as follows for p=1 in this illustration:

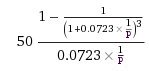
The two formulas are equivalent only in the special case where p=1 is the number of annuity payments per year. In the general case when p>1, the latter formula would put in the correct m and the two formulas would not be equivalent.

For illustrative purposes I will focus on the following example on Page 11 of Professor Deeley's working paper ---
http://www.cs.trinity.edu/~rjensen/temp/DeeleyAnnuityCorrections.pdf

Example 2
A loan of $1million is to be repaid in equal monthly installments over four years. If the annual interest rate is 10% compounded semi-annually, how much is the monthly repayment?

m=2 interest compoundings per year

p=12 monthly payments per year

n=48 monthly payments over four years

PV=$1,000,000 present value

i=0.10 annual interest rate in the annuity contract

For the CFA Deconstruction solution we compute an equivalent i' interest rate to use in place of the i=0.10 rate. We get the following:

i' = 0.1025
=(1+0.10/2)^(2) - 1

CFA Deconstruction PMT = $25,483 per month which conforms to David Frick's solution tutorial
=1000000/((1-(1+0.1025/12)^(-48))/(0.1025/12))